Про наукові роботи учнів – учасників
конкурсу-захисту МАН України.
Володимир Плахотник
Основна проблема, з якою стикається відділення математики Малої академії наук України – проблема банку задач, які могли б бути основою для наукової роботи учнів. Далеко не в кожній області є ентузіасти, які здатні і мають бажання поставити цікаві математичні задачі чи керувати їх розв’язанням. Саме тому на заключний, третій етап конкурсу-захисту часто попадають відверто задачі слабкі, що не можуть бути названі науковими.
Кожен учень, який задумався про наукову роботу, має аналогічну проблему: де знайти наукового керівника і де знайти задачу, при розв’язуванні якої можна було б узнати про наявність принаймні деяких здібностей до наукової роботи. Багато здібних дітей могли б і самостійно відповісти на деякі запитання, якби знали, на які саме.
На сторінках видання “У світі математики” пропонується ввести цикл публікацій, які б містили постановки принаймні невеликої кількості задач дослідницького характеру. Чи вийде з кожної запропонованої задачі наукова робота, стане ясно тільки після того, як буде отримано якусь конкретну цікаву відповідь на поставлені запитання.
Кілька можливих робіт для учасників конкурсу-захисту Малої Академії Наук України пропонується цьому номері журналу. Роботи розраховані на учнів 9-11 класів. Автор запрошує інших вчених-математиків взяти участь у аналогічній роботі. Бажано, щоб запропоновані задачі були авторськими, щоб постановка задачі супроводжувалась принаймні деякими позитивними кроками у напрямку до розв’язання задачі. Ясно, що публікація задачі в цьому журналі або у якомусь іншому, зробить можливим для учнів звернутись до автора задачі з проханням про керівництво, або знайти собі іншого керівника і автори задач повинні розуміти, що обидва випадки цілком можливі. Але, у будь-якому разі, авторство постановки задачі збережеться.
Задача 1. Про двосторонню оцінку деяких послідовністей.
Нехай ![]() і
і ![]() – довільні арифметичні чи якісь іннші числові послідовності. Розглянемо добуток
– довільні арифметичні чи якісь іннші числові послідовності. Розглянемо добуток
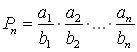 .
.
Знайти елементарні функції ![]() та
та ![]() , щоб для усіх натуральних значень
, щоб для усіх натуральних значень ![]() , починаючи з деякого номера, справджувалась нерівність
, починаючи з деякого номера, справджувалась нерівність ![]() і така оцінка була якомога “кращою”.
і така оцінка була якомога “кращою”.
Приклади. 1. Розглянемо послідовність чисел ![]() , для якої
, для якої ![]() . Виявляється, для цієї послідовності існує нерівність
. Виявляється, для цієї послідовності існує нерівність 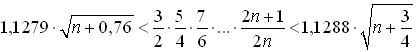 , правильна при
, правильна при ![]() .
.
2. Розглянемо послідовність чисел ![]() , для якої
, для якої ![]() . Виявляється, для цієї послідовності існує нерівність,
. Виявляється, для цієї послідовності існує нерівність, 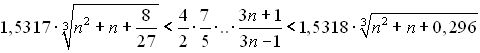 , правильна при
, правильна при ![]() .
.
3. Розглянемо послідовність чисел ![]() , для якої
, для якої ![]() . Виявляється, для цієї послідовності існує нерівність
. Виявляється, для цієї послідовності існує нерівність ![]() , правильна при
, правильна при ![]() .
.
Задача полягає в тому, щоб знайти подібні або складніші нерівності і помітити якісь загальні закономірності.
Так, наприклад, наступне твердження легко доводиться за індукцією.
Теорема. При довільних натуральних ![]() і довільному дійсному
і довільному дійсному ![]() справджується нерівність
справджується нерівність
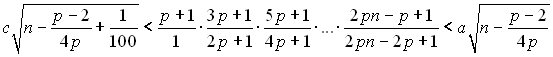 ,
,
де для чисел ![]() справджуються умови
справджуються умови
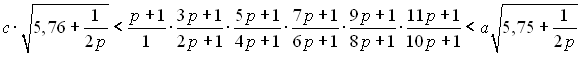 .
.
Найважча частина роботи – передбачити, який вигляд мають функції ![]() та
та ![]() . Якщо правильно “вгадати” відповідь, доведення, найбільш ймовірно, не викликатиме суттєвих проблем.
. Якщо правильно “вгадати” відповідь, доведення, найбільш ймовірно, не викликатиме суттєвих проблем.
Задача 2. Про діагоналі, сторони і кути правильного многокутника.
При проведенні кожної діагоналі опуклого многокутника утворюється два опуклих многокутники. Позначимо через ![]() кількість вершин того із них, у якому ця кількість менша, і будемо називати число
кількість вершин того із них, у якому ця кількість менша, і будемо називати число ![]() типом проведеної діагоналі. Так, наприклад, кожна діагональ опуклого чотирикутника чи п’ятикутника має тип 3. Легко зрозуміти, що при
типом проведеної діагоналі. Так, наприклад, кожна діагональ опуклого чотирикутника чи п’ятикутника має тип 3. Легко зрозуміти, що при ![]() в опуклому
в опуклому ![]() -кутнику тип діагоналі може набувати довільного цілого значення від 3 до
-кутнику тип діагоналі може набувати довільного цілого значення від 3 до 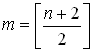 .
.
У правильному ![]() -кутнику всі внутрішні кути рівні між собою, всі сторони рівні між собою і рівні між собою всі діагоналі кожного із можливих типів. Правильне й обернене твердження, тобто з рівності усіх сторін, усіх внутрішніх кутів і усіх діагоналей кожного можливого типу для даного числа
-кутнику всі внутрішні кути рівні між собою, всі сторони рівні між собою і рівні між собою всі діагоналі кожного із можливих типів. Правильне й обернене твердження, тобто з рівності усіх сторін, усіх внутрішніх кутів і усіх діагоналей кожного можливого типу для даного числа ![]() випливає, що опуклий
випливає, що опуклий ![]() -кутник буде правильним. Чи не можна послабити цей очевидний, але непотрібний критерій правильності
-кутник буде правильним. Чи не можна послабити цей очевидний, але непотрібний критерій правильності ![]() -кутника і вимагати, щоб не всі внутрішні кути, сторони чи діагоналі певного типу були рівними між собою відповідно, а лише деякі з них?
-кутника і вимагати, щоб не всі внутрішні кути, сторони чи діагоналі певного типу були рівними між собою відповідно, а лише деякі з них?
Для прикладу розглянемо випадок ![]() .
.
Якщо вимагати рівність усіх кутів, рівність двох сторін і рівність обох діагоналей, дістанемо чотирикутник, який не обов’язково є квадратом, бо таким чотирикутником може бути й прямокутник.
Якщо у чотирикутнику є три рівних сторони, два рівних внутрішні кути і рівні діагоналі, такий опуклий чотирикутник також не обов’язково буде квадратом. Контрприкладом є рівнобічна трапеція, у якій одна із основ дорівнює бічній стороні.
Якщо ж вимагати рівність усіх сторін і рівність обох діагоналей, дістанемо чотирикутник, який є квадратом, як ромб з рівними діагоналями.
Якщо у чотирикутнику є три рівних сторони і три рівних внутрішні кути, такий опуклий чотирикутник також обов’язково буде квадратом. Доведення цього факту достатньо просте. Досить розглянути два різних випадки розмішення рівних кутів відносно рівних сторін.
Ці приклади дають повний опис випадків, коли при наявності певної кількості попарно рівних сторін, кутів та діагоналей певного типу опуклий
4-кутник обов’язково буде квадратом.
Щоб було зручно формулювати постановку задачі у загальному випадку, введемо деякі позначення.
Так, індексом множини всіх опуклих ![]() -кутників, у яких є не менше
-кутників, у яких є не менше ![]() рівних внутрішніх кутів, не менше
рівних внутрішніх кутів, не менше ![]() рівних сторін, не менше
рівних сторін, не менше ![]() рівних діагоналей типу 3, …., не менше
рівних діагоналей типу 3, …., не менше ![]() рівних діагоналей типу
рівних діагоналей типу ![]() , називатимемо вектор
, називатимемо вектор
![]() .
.
Якщо усі ![]() -кутники цієї множини – правильні, множину будемо називати тривіальною, а її індекс – тривіальним. Так, враховуючи сказане вище про випадок
-кутники цієї множини – правильні, множину будемо називати тривіальною, а її індекс – тривіальним. Так, враховуючи сказане вище про випадок ![]() , бачимо, що індекси
, бачимо, що індекси ![]() і
і ![]() є тривіальними, а індекси
є тривіальними, а індекси ![]() і
і ![]() не є тривіальними.
не є тривіальними.
Метою даної роботи є опис усіх тривіальних і усіх нетривіальних індексів.
Оскільки при виконанні усіх нерівностей
![]()
з тривіальності індекса ![]() випливає тривіальність індекса
випливає тривіальність індекса ![]() , а з нетривіальності індекса
, а з нетривіальності індекса ![]() випливає нетривіальність індекса
випливає нетривіальність індекса ![]() , для опису всіх тривіальних індексів досить описати мінімальні (у природному сенсі) тривіальні індекси, а для опису всіх нетривіальних індексів досить описати максимальні нетривіальні індекси.
, для опису всіх тривіальних індексів досить описати мінімальні (у природному сенсі) тривіальні індекси, а для опису всіх нетривіальних індексів досить описати максимальні нетривіальні індекси.
Із сказаного вище випливає що у випадку ![]() множина мінімальних тривіальних індексів має два елементи
множина мінімальних тривіальних індексів має два елементи ![]() і
і ![]() , а множина максимальних нетривіальних індексів має два елементи
, а множина максимальних нетривіальних індексів має два елементи ![]() і
і ![]() .
.
Отже, найпростішою, ще нерозв’язаною на даний момент задачею є опис усіх мінімальних тривіальних і максимальних нетривіальних індексів у випадку ![]() . Опису таких індексів і може бути присв’ячена пропонована наукова робота.
. Опису таких індексів і може бути присв’ячена пропонована наукова робота.
Задача 3. Про суми квадратів кількох послідовних натуральних чисел.
Чи може сума квадратів кількох послідовних натуральних чисел бути квадратом натурального числа? Природно, що відповідь залежить від того, скільки саме доданків містить сума (далі кількість доданків позначатимемо через ![]() ). Ясно, що першою згадується рівність
). Ясно, що першою згадується рівність ![]() у випадку
у випадку ![]() . Однак навряд чи кожен може навести без обдумування принаймні ще один приклад. Втім, таких прикладів досить багато. Ось деякі з них:
. Однак навряд чи кожен може навести без обдумування принаймні ще один приклад. Втім, таких прикладів досить багато. Ось деякі з них:
![]()
![]() ,
, ![]()
![]() ,
, ![]()
![]() ,
, ![]()
![]() ,
,
![]()
![]() ,
, ![]()
![]() ,
, ![]()
![]() .
.
Знайти такі співвідношення для фіксованої кількості доданків ![]() – не дуже складно. Однак, для цього потрібно знати алгоритм розв’язування рівняння Пеля і узагальненого рівняння Пеля. Для зацікавлення читача спочатку наведемо помічені факти.
– не дуже складно. Однак, для цього потрібно знати алгоритм розв’язування рівняння Пеля і узагальненого рівняння Пеля. Для зацікавлення читача спочатку наведемо помічені факти.
Виявляється, для багатьох ![]() шуканих сум взагалі не існує. Прикладами можуть бути
шуканих сум взагалі не існує. Прикладами можуть бути ![]() та інші. Є значення
та інші. Є значення ![]() , для яких існує єдина сума. Так, при
, для яких існує єдина сума. Так, при ![]() і
і ![]() наведені вище суми єдині. Є значення
наведені вище суми єдині. Є значення ![]() , для яких існує скінченна, більша за одиницю кількість сум. Так, існує рівно 7(сім) сум квадратів таких двохсот вісімдесяти дев’яти послідовних натуральних чисел, що кожна сума дорівнює квадратові натурального числа. Ось усі ці суми:
, для яких існує скінченна, більша за одиницю кількість сум. Так, існує рівно 7(сім) сум квадратів таких двохсот вісімдесяти дев’яти послідовних натуральних чисел, що кожна сума дорівнює квадратові натурального числа. Ось усі ці суми: ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
,
![]() .
.
Зауважимо, що кількість сум може бути й парною. Так, існує рівно десять сум квадратів дев’ятисот шестидесяти одного послідовних натуральних чисел, таких що кожна сума дорівнює квадратові натурального числа. “Найменша і найбільша” з них мають відповідно вигляд
![]() і
і ![]() .
.
І, нарешті, є значення ![]() , для кожного із яких існує нескінченно багато сум.
, для кожного із яких існує нескінченно багато сум.
Так, при ![]() усі суми у певному сенсі є узагальненнями однієї з двох сум, наведених спочатку. А для відшукання всіх сум вигляду
усі суми у певному сенсі є узагальненнями однієї з двох сум, наведених спочатку. А для відшукання всіх сум вигляду
![]()
потрібно скористатись рекурентними формулами
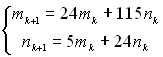 ,
,
де ![]() або
або ![]() .
.
В такий спосіб дістанемо суми ![]() ,
,
![]() та інші.
та інші.
Задача полягає у тому, щоб описати усі значення ![]() , для яких існують суми
, для яких існують суми ![]() послідовних квадратів натуральних чисел, кожна із яких є квадратом цілого числа. Або, принаймні, знайти якісь загальні закономірності. Якщо не вийде повна відповідь, можна надіятись відшукати всі значення
послідовних квадратів натуральних чисел, кожна із яких є квадратом цілого числа. Або, принаймні, знайти якісь загальні закономірності. Якщо не вийде повна відповідь, можна надіятись відшукати всі значення ![]() , де
, де ![]() якесь достатньо велике натуральне число, наприклад,
якесь достатньо велике натуральне число, наприклад, ![]() .
.
Так, наприклад, доведено таке твердження.
Теорема. Якщо ![]() або
або ![]() , то сума
, то сума ![]() квадратів послідовних натуральних чисел не може бути квадратом цілого числа.
квадратів послідовних натуральних чисел не може бути квадратом цілого числа.
Доведення. Якщо ![]() ,
,
то після використання формули ![]()
дістанемо рівність ![]() , яку розглянемо по модулю 4.
, яку розглянемо по модулю 4.
Оскільки ![]() , отримаємо рівносильну умову
, отримаємо рівносильну умову ![]() .
.
Якщо тепер ![]() або
або ![]() , то
, то ![]() або
або ![]() . У обох випадках дістанемо суперечність, і теорему доведено.
. У обох випадках дістанемо суперечність, і теорему доведено.
У кожній із трьох розглянутих вище задач можливі й інші, не вказані автором запитання, відповідь на які представляє інтерес. Які саме запитання, може стати зрозумілим у процесі вивчення, розв’язування задачі, пошуку відповіді на уже поставлені завдання.